 by FrediFizzx » Sun Oct 11, 2015 11:41 pm
by FrediFizzx » Sun Oct 11, 2015 11:41 pm
Recently on
Albert Jan's Blog, we discovered that quantum theory cannot produce the negative cosine curve using +/-1 outcomes. So, how to best simulate what is going on in an EPR-Bohm scenario? It seems that one is forced to use some kind of hidden variable model to do it. Of course if anyone thinks they can do it without hidden variables, please post it here.

So I was playing around with John Reed's Mathematica version of Michel's epr-simple simulation and discovered that it can produce the -cosine curve without using the angle "e" for the particles. It now depends only on lambda, a and b. So the particles are only "carrying" lambda. Here are the links;
EPRsims/EPRBsimJC_JR_MF.nb Mathematica notebook file.
EPRsims/EPRBsimJC_JR_MF1.pdf PDF of notebook with results
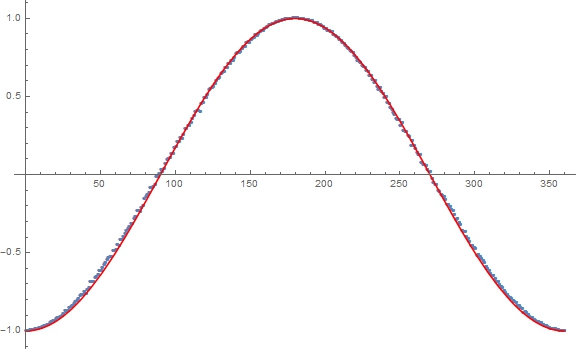
So this may be the most simple way to simulate EPR-Bohm giving the full -cosine curve using +/-1 outcomes for A and B with one degree resolution for the a and b angle difference. Of course Joy's S^3 simulations probably have the best
physics explanation.
Recently on [url=http://challengingbell.blogspot.com/2015/06/a-flatlanders-view-on-joy-christians.html]Albert Jan's Blog[/url], we discovered that quantum theory cannot produce the negative cosine curve using +/-1 outcomes. So, how to best simulate what is going on in an EPR-Bohm scenario? It seems that one is forced to use some kind of hidden variable model to do it. Of course if anyone thinks they can do it without hidden variables, please post it here. :D
So I was playing around with John Reed's Mathematica version of Michel's epr-simple simulation and discovered that it can produce the -cosine curve without using the angle "e" for the particles. It now depends only on lambda, a and b. So the particles are only "carrying" lambda. Here are the links;
http://www.sciphysicsforums.com/spfbb1/EPRsims/EPRBsimJC_JR_MF.nb Mathematica notebook file.
http://www.sciphysicsforums.com/spfbb1/EPRsims/EPRBsimJC_JR_MF1.pdf PDF of notebook with results
[img]http://www.sciphysicsforums.com/spfbb1/EPRsims/EPRBsimJC_JR_MF.jpg[/img]
So this may be the most simple way to simulate EPR-Bohm giving the full -cosine curve using +/-1 outcomes for A and B with one degree resolution for the a and b angle difference. Of course Joy's S^3 simulations probably have the best [b]physics [/b]explanation.
