Justo wrote:Joy Christian wrote:Then the hidden variable version of the QM equation < A > + < B > = < A + B > is not < a > + < b > = < a + b >, but < a > + < b > = < c >.
That is right when we interpret <A + B> as the mean corresponding to the observable A+B. However, in the Bell inequality, we are not dealing with the operator A + B. The quantum observable A + B is not an issue in the Bell inequality, not even when calculating the quantum prediction. Only the individual observables A and B are evaluated.
In the Bell-test experiments, we
are dealing with non-commuting operators. Bell explicitly writes
John S. Bell wrote:Consider a pair of spin one-half particles formed somehow in the singlet spin state and moving freely in opposite directions. Measurements can be made, say by Stern-Gerlach magnets, on selected components of the Spins
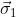
and
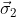
, If measurement Of the component
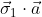
, where
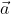
is some unit vector, yields the value + 1 then, according to quantum mechanics, measurement of
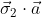
must yield the value -1 and vice versa.
Evidently,
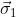
and
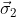
are quantum mechanical operators, and (in Bell's notation) A = +/-1 and B = +/-1 are eigenvalues of these operators.
Justo wrote:
The Bell inequality only concerns the means of the separate observables A and B and what hidden variables predict for <A> + <B>, then we write <A> + <B> = whatever valid mathematical operations allowing us to evaluate <A> + <B>.
The valid mathematical operation is physically meaningless. That is the point of Einstein's, Bell's, and many other scholar's criticisms of von Neumann who used the "valid mathematical operation < A + B >" to derive his conclusion. Bell, after ridiculing von Neumann, went on to use the same physically meaningless mathematical operation to derive Boole's 100-years old inequality, and then made outrageous metaphysical claims based on his incorrect derivation.
Justo wrote:
Therefore when Bell wrote <A> + <B> = <A + B> he is not assuming that the eigenvalue of the operator A + B is sum of the individual eigenvalues. Again, the observable A + B is not under consideration when dealing with the Bell inequality.
This is not correct. Bell is implicitly assuming precisely what you are claiming he is not assuming. The meaning of A + B is quite clear from the above quotation from Bell's 1964 paper.
Justo wrote:
It is the same old problem with the Bell inequality: misinterpreting valid mathematical operations and giving them literal and incorrect physical interpretations.
This is quite correct. You, like many others, have misinterpreted both Bell's inequality and its physical meaning. For its correct interpretation, please read my paper I have linked above.
------------------------------------------------------
PS: For those who do not have time to read my paper, here is the upshot of it. For whatever reason, Bell's derivation of his inequalities involves the additivity of expectation values:
< A > + < B > = < A + B >.
This is an assumption. Whether it is a justified assumption or not is irrelevant. What matters is that without this assumption the derivation of Bell inequalities does not go through.
Now we do the experiments and discover that the bounds of +/-2 on the Bell-CHSH inequalities are exceeded. The only rational conclusion from that is to conclude that the assumption of the additivity of expectation values is ruled out by the experiments. Anything else is pure speculation.
.


