Definition of "realistic" in "local-realistic"
The present posting replies to the following quote of Fredifizzx
I doubt that there is substantial agreement that Dr. Christian's
model can be considered "local-realistic". By a "realistic" model,
I think most people mean a model in which all measurements are detecting
something which is "really" there. By "really there",
we mean that the model allows us to measure,
in principle, all measurable quantities simultaneously.
For example, suppose Alice can measure quantities named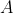 and
and 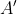 ,
,
obtaining in each measurement (say) +1 or -1. But she may not be able
to measure them simultaneouly, due to limitations in her equipment
or to some physical law. If she cannot, one could argue that
when she measures does not exist in any verifiable sense, and vice versa.
does not exist in any verifiable sense, and vice versa.
In that case, when she measures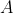 , there will exist a probability function
, there will exist a probability function )
which gives a probability) that she measures
that she measures  and a probability
and a probability
) that she measures
that she measures 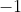 . If we idealize to assume that there
. If we idealize to assume that there
are no "dud" measurements which yield no result, we will have
 + p_A(-1) = 1.) Of course, there will exist a similar probability
Of course, there will exist a similar probability
function) for when she chooses to measure
for when she chooses to measure 
BUT THERE WILL BE NO OBVIOUS REASON TO ASSUME THAT THERE EXISTS A JOINT
PROBABILITY FUNCTION) for which
for which 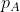 and
and  are marginals.
are marginals.
Such a joint probability function would give, for example,
a probability) that
that 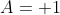 and
and  etc.
etc.
To say that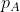 is a marginal for
is a marginal for  means, for example,
means, for example,
that = p_{AA'}(-1,+1) + p_{AA'}(-1,-1).)
A model for which there does exist such a joint probability function
is called a *realistic* model, because it allows the possibility
that both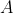 and
and 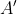 have definite values even if in practice we can't observe
have definite values even if in practice we can't observe
these values simultaneously.
It is a simple exercise to derive a necessary and sufficient
condition for two given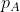 and
and  to be the marginals of some
to be the marginals of some 
It turns out that the condition is always satisfied, so for this simple
case, every model is "realistic". But in the more general case which will
be considered next, this will not hold.
Next consider two observers Alice and Bob, each of whom can make
measurements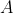 or
or 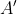 for Alice, or
for Alice, or 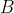 or
or 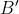 for Bob, as described above.
for Bob, as described above.
Then there are four possible measurements for both together, which we may
denote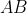 ,
,  ,
,  ,
,  , with corresponding joint probability distributions
, with corresponding joint probability distributions
) ,
, ,) etc. The generally accepted definition
etc. The generally accepted definition
of a "realistic" model is one for which corresponding to these four given
joint distributions, there exists a probability distribution)
for which the given are marginals.
are marginals.
This means, for example, that the probability that is
is ,) and that
and that
where the symbols i and j range over the set .
.
and similarly for) , etc.
, etc.
The usual proof of the CHSH "Bell'' inequalities shows that
a necessary condition for the existence of is for the CHSH
is for the CHSH
inequalities to hold. That is, CHSH is a necessary condition for the
existence of a "realistic" model, as "realistic" is usually defined.
The model of quantum mechanics does not satisfy the CHSH inequalities,
and therefore, by this definition, is not "realistic". Neither is Christian's
model "realistic" according to this definition, since it makes predictions identical to
quantum mechanics (at least for the singlet state, which seems to be all that is considered
in this forum). These are simple mathematical facts about which, so far as I know,
there is no controversy whatsoever.
Apparently, some of the posters in this group believe that
Christian's model is "locally realistic" (hence "realistic"). For this to
be correct, they have to be using a different definition of "realistic",
which has never been made explicit, so far as I know.
Readers interested in exploring this further may find the following
of interest:
A. Fine, "Hidden variables, joint probability and the Bell inequalities"
Phys. Rev. Lett. 48 (1982), 291-295
A. Fine, "Joint distributions, quantum correlations, and commuting
observables", J. Math. Phys. 23 (1982), 1306-1310
For the discussion above, these papers merely validate that our definition
of a "realistic" model is a commonly accepted one. Actually, Fine
proves in both papers the converse of the mathematically trivial fact
that the CHSH inequalities are a necessary condition for a realistic model.
Fine proves the much more difficult result that satisfaction of
the CHSH inequalities is sufficient for a model to be "realistic" in
the sense described above. The mathematical contents of the above two
papers are similar, but I think that the second is much easier to read.
2. It is a proven fact that Joy Christian's local-realistic model is a valid counter example to Bell's so-called "theorem". Therefore all of Bell's arguments are invalid. It is junk physics now.
FrediFizzx
Independent Physics Researcher
I doubt that there is substantial agreement that Dr. Christian's
model can be considered "local-realistic". By a "realistic" model,
I think most people mean a model in which all measurements are detecting
something which is "really" there. By "really there",
we mean that the model allows us to measure,
in principle, all measurable quantities simultaneously.
For example, suppose Alice can measure quantities named
obtaining in each measurement (say) +1 or -1. But she may not be able
to measure them simultaneouly, due to limitations in her equipment
or to some physical law. If she cannot, one could argue that
when she measures
In that case, when she measures
which gives a probability
are no "dud" measurements which yield no result, we will have
function
BUT THERE WILL BE NO OBVIOUS REASON TO ASSUME THAT THERE EXISTS A JOINT
PROBABILITY FUNCTION
Such a joint probability function would give, for example,
a probability
To say that
that
A model for which there does exist such a joint probability function
is called a *realistic* model, because it allows the possibility
that both
these values simultaneously.
It is a simple exercise to derive a necessary and sufficient
condition for two given
It turns out that the condition is always satisfied, so for this simple
case, every model is "realistic". But in the more general case which will
be considered next, this will not hold.
Next consider two observers Alice and Bob, each of whom can make
measurements
Then there are four possible measurements for both together, which we may
denote
of a "realistic" model is one for which corresponding to these four given
joint distributions, there exists a probability distribution
for which the given
This means, for example, that the probability that
where the symbols i and j range over the set
and similarly for
The usual proof of the CHSH "Bell'' inequalities shows that
a necessary condition for the existence of
inequalities to hold. That is, CHSH is a necessary condition for the
existence of a "realistic" model, as "realistic" is usually defined.
The model of quantum mechanics does not satisfy the CHSH inequalities,
and therefore, by this definition, is not "realistic". Neither is Christian's
model "realistic" according to this definition, since it makes predictions identical to
quantum mechanics (at least for the singlet state, which seems to be all that is considered
in this forum). These are simple mathematical facts about which, so far as I know,
there is no controversy whatsoever.
Apparently, some of the posters in this group believe that
Christian's model is "locally realistic" (hence "realistic"). For this to
be correct, they have to be using a different definition of "realistic",
which has never been made explicit, so far as I know.
Readers interested in exploring this further may find the following
of interest:
A. Fine, "Hidden variables, joint probability and the Bell inequalities"
Phys. Rev. Lett. 48 (1982), 291-295
A. Fine, "Joint distributions, quantum correlations, and commuting
observables", J. Math. Phys. 23 (1982), 1306-1310
For the discussion above, these papers merely validate that our definition
of a "realistic" model is a commonly accepted one. Actually, Fine
proves in both papers the converse of the mathematically trivial fact
that the CHSH inequalities are a necessary condition for a realistic model.
Fine proves the much more difficult result that satisfaction of
the CHSH inequalities is sufficient for a model to be "realistic" in
the sense described above. The mathematical contents of the above two
papers are similar, but I think that the second is much easier to read.


