Bell's equalities
On these forums, we have spent many years arguing about inequalities. But do we really understand what they mean? I'm becoming convinced that often, inequalities are easy to misinterpret because they are by definition incomplete mathematical expressions. For example the expression
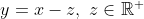
can be written in incomplete form as
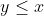
But this obscures the claim about
Some times, the terms needed to understand the meaning of the inequality are precisely the ones that have been hidden/removed. So in this thread, I'm hoping we would carry out a simple exercise with Bell's inequality. For Bell's theorem, using the wikipedia form:
 - C_h(b, a) - C_h(b, c) \le 1)
In other words using my earlier symbols:
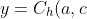 - C_h(b, a) - C_h(b, c))
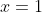
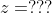
What is ?
?
Let us complete the expression with the full form of z. Let us do the derivation of the equality rather than the inequality. Once we are done, let us examine what it means to say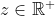 .
.
 - C_h(b, a) - C_h(b, c) = 1 + z)
can be written in incomplete form as
But this obscures the claim about
Some times, the terms needed to understand the meaning of the inequality are precisely the ones that have been hidden/removed. So in this thread, I'm hoping we would carry out a simple exercise with Bell's inequality. For Bell's theorem, using the wikipedia form:
In other words using my earlier symbols:
What is
Let us complete the expression with the full form of z. Let us do the derivation of the equality rather than the inequality. Once we are done, let us examine what it means to say