Gordon Watson wrote:I take probability theory (PT) to be the logic of science. (And I like the related math to do much of my talking.) PT allows me to encode incomplete information, en route to establishing more complete information.
That's not what the phrase "Logic of Science" is supposed to mean when referring to PT. It doesn't mean non-probabilistic answers are illogical.
So I am not saying that I don't know how the transformation happens. In my view, under EPRB, particle-polariser interactions expose the equivalence class (EC) to which each incoming (pristine) particle belonged.
How? Either you know how and don't want to tell us, or you don't know how and don't want to tell us.
If I say
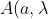 = sign(a \cdot \lambda))
, I've provided exactly how
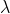
is transformed together with the setting

to generate the outcomes

. Then I've also shown that there are just two equivalence classes of lambda, as there must be because we already know that the outcomes can only be one of

by definition. The important point about specifying the
mechanism of transformation is to show how the
universe of vectors
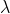
are divided into the two equivalence classes.
However, if I refuse to provide the
mechanism (aka details of the function) and just insist that there are equivalence classes, I would have added zero content to the Bell discussion.
I don't see that my focus on ECs is excessive. As for the Bell literature, please show me a tested
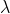
that did not reveal an EC. It seems to me that it would not be EPRB if a
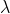
produced other than a specific outcome?
I think you miss the point. It is not that ECs are lacking, but that they are so obvious as to be uninteresting for the analysis. Bell introduces equivalence classes by definition. The interesting part is not the presence of ECs but in specifying which
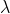
belong to the same equivalence class in the context of a setting

. And you show that by presenting the functions, otherwise talking about ECs is uninteresting.
Yes, I struggle with
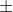
, superscripted or otherwise! Reason: I believe, (i) we advance teaching and understanding when we expose symmetries; (ii) we clarify Bell's ideas when we use the licence given by Bell at the end of II. Formulation; (iii) it seems that my shorthand needs to be clearer.
Who is it are you trying to teach? Have you figured that these purported students need to learn about symmetry at the same time as trying to understand a topic for which symmetry so obvious as to not be interesting? A good teacher shows focus and restraint when conveying information. Just because you are thinking about it doesn't mean it needs to be written down. What exactly is the main point you want to make. Focus on that. If your brain is overflowing with great ideas, write many different papers, each one focused on one key idea.
I'm inclined to return as close as is sensible to Bell's notation. The ECs are not probabilistic; my knowledge of them is.
So you don't know what the functions are, contrary to what you wrote above? I'm confused.
Thanks for the offer of specific vectors. Maybe I need to be clearer that I use that term in the context of GA.
Geometric Algebra allows you to do analysis in a coordinate-free manner. It doesn't mean you wouldn't know what to do with coordinates when given.
But see here how I use PT: The probability of you knowing such a variable is zero. However, if you are a lab-mate of mine that tests twins, the probability that you know the EC of the particle that is on its way to me is non-zero. So best offer that very helpful EC.
That's actually very funny, or sad depending on your perspective. By providing them to you, you have to assume that I know them so saying I can't possibly know them, is not a reason for not answering my question. What if I knew them, how would you proceed? If you know the
mechanics of your functions this question should be very easy.
For me, I feel that I took the better view: that it was better to seek functions that were informative and hopeful. Not one that was false and inappropriate.
Are you still seeking these functions or have you found them already?
It seems to me, the ECs are all about the dynamics.
And the details of the functions show how the ECs are generated. So the dynamics are in the functions, not the ECs.
PS: It would help me greatly if (where sensible) you limited each post to a single issue. That would help me answer earlier and more expansively when I'm pressed for time.
Feel free to respond to just one issue at a time. I just prefer to respond in this way especially since I want to respond in one seating without having to deal with the rate-limit.
superscripts for
are superfluous and confusing?? Otherwise please explain what the following means:

