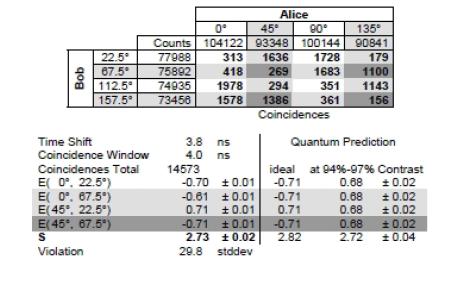
Heinera wrote:But it is. Given some large N, you are suggesting that restricting the correlation computation on N pairs of numbers to an N/4 random subset of those pairs somehow gives you a significantly different correlation, are you not?
No. I'm saying the relationship between two correlated variables from the exact same set should not be expected to hold between to two variables from completely disjoint sets. You are getting confused by Richard's N and missed the point in this statement:
minkwe wrote:The height of the 250000 people is not a independent free variable from the weight of the same 250000 people. However, the height of the 250000 people is an independent free variable from the weight of another 250000 completely different people drawn from the same population.
Do you expect outcomes from one set of particle pairs to be correlated with outcomes from a completely different set of particle pairs? If you measure them all on the same set, you would expect correlations between them. If you measure them on different sets you shouldn't, even if you are measuring the same type of properties at the same angles. It is that simple.
If you measure E(a,b), E(a,b'), E(a',b') and E(a',b) all from a single set of particle pairs, you would expect those expectation values to be correlated. If you measure them each from a different set of particle pairs, you shouldn't expect the same correlations between them to be present. It is that simple.